본문으로 바로가기

CS 18일차

category CS 공부/CS Study 원본 2021. 2. 22. 22:37

async vs sync / blocking vs non-blocking

mangocode.tistory.com/84

(17차 스터디에서 진행)

 

KMP 알고리즘 (출처 - baeharam.github.io/posts/algorithm/kmp/ )

 

KMP 알고리즘은 어떤 문자열 HH와 SS가 주어졌고 HH가 SS보다 긴 경우에, HH 안에 SS가 포함되어 있는지를 탐색하는 알고리즘이다. 자, 생각을 해보자. 예를 들어 단순 브루트 포스로 SS를 탐색한다면 상당히 오랜 시간이 걸릴 수밖에 없다.

예를 들어, ABAABAA라는 문자열 HH에서 부분문자열 ABAC를 찾기 위해선 아래와 같이 찾아야 한다.

당연하게도 시간복잡도는 HH의 길이를 n, SS의 길이를 m이라고 했을 때 O(nm)O(nm)이 나오게 되기 때문에 비효율적이라는 것을 한눈에 알 수 있다. 그럼 어떻게 개선할 수 있을까?

위 그림에서 처음 비교를 할 때 ABA까지는 일치하지만 C에서 불일치한다는 것을 볼 수 있다. KMP는 이 점을 착안해서 ABA까지 일치하니까 인덱스를 1만 옮기지 말고, 일치한 부분은 옮겨도 된다고 말한다. 즉, 이미 얻은 정보를 활용하여 문자열 SS를 빠르게 옮기는 것이다.

핵심 개념

그럼 위에서 말한대로 ABA까지 일치하니까 한번에 옮기면 되는 것일까? 아래 그림을 보자.

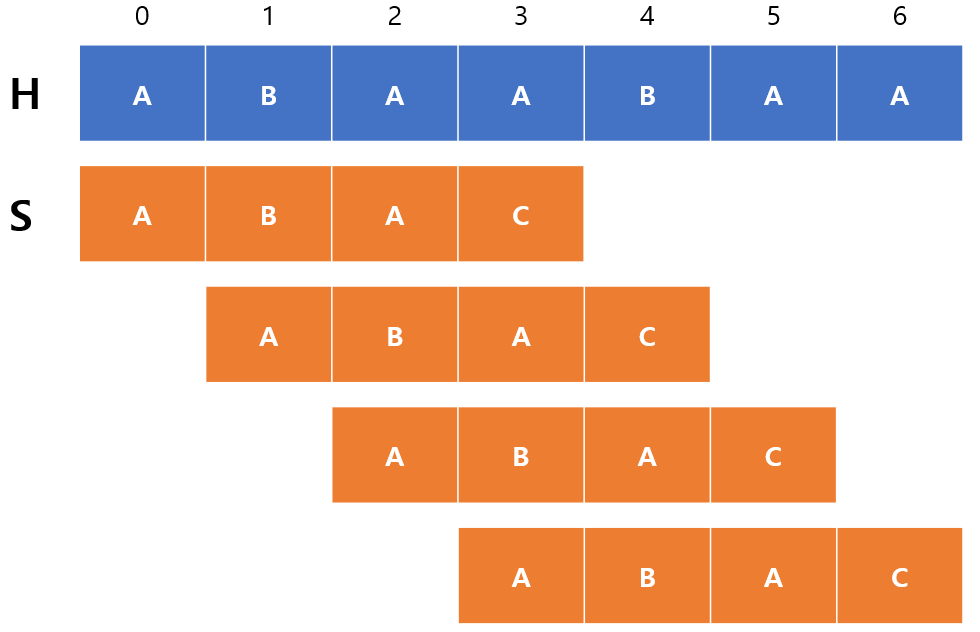
ABA를 건너뛰고 한번에 옮겼더니 원래 계산해야 될 1번째,2번째 인덱스를 생략할 수 있었다. 그러나 빼먹은 부분이 있으니 바로 ABA는 반복되는 부분문자열이 있다는 것이다.

이 말은 ABA가 일치하긴 해도 그 안에 SS가 시작할 수 있는 부분이 존재할 여지가 있기 때문에 반드시 ABA에서 시작할 수 있는지 없는지를 확인해주어야 한다.

그렇다면 어디에서 시작해야 할까? 접두사와 일치하는 접미사가 있는지를 확인해주면 된다. 왜냐하면 일치하는 문자열은 이미 SS에 속한 문자열이기 때문에 또다른 SS의 시작점을 찾는 것이 핵심이기 때문이다. 그 시작점을 찾는 것이 바로 접미사에서 접두사와 같은 부분이 있는지를 확인하는 것임을 알 수 있다.

ABA는 A가 접미사이면서 접두사가 되기 때문에 앞쪽의 AB를 건너뛸 수 있게 되므로 아래그림과 같이 2번째 인덱스부터 비교하면 되는 것이다.

결국 이 말은 SS에서 0번째 인덱스를 제외한 다른 인덱스들에 대해 접두사와 접미사가 일치하는 부분을 알아야 한다는 것이다. 그래야 그만큼을 탐색하지 않고 건너뛸 수 있기 때문에 따로 그 값을 미리 구해놓아야 한다. (0번째 인덱스를 제외하는 이유는 문자 1개밖에 없기 때문)

이 값을 사용하는 경우는 불일치가 발생했을 때 이기 때문에, 실패했을 때 어떻게 해야하는지 알려준다는 점에서 실패 함수(failure function)라고 부르기도 한다.

★ 실패 함수

실패 함수는 KMP에서 아주 중요한 개념이고 상당히 많이 활용되기 때문에 반드시 익혀야 한다. 이번엔 예시를 좀 변경해서 SS를 좀 더 긴 문자열로 잡고 실패 함수값을 구해보자. SS를 ABABAB라고 하고 실패 함수를 F(k)F(k)라고 하면, F(k)F(k)의 의미는 kk번째 인덱스에서 접두사와 접미사가 일치하는 최대길이이다. (최대인 이유는 굳이 최대로 일치하는 부분이 있음에도 불구하고 그것보다 작은 길이 만큼 건너뛰는 것은 낭비이기 때문)

위에서 말했던 것처럼 0번째 인덱스는 스킵하고 1번째 인덱스부터 보면 AB에서 접두사,접미사가 일치하는 부분이 없기 때문에 F(1)=0F(1)=0이다.

다음으로 ABA에선 A가 최대로 일치하는 부분이므로 F(2)=1F(2)=1이다.

그 다음은 ABAB이기 때문에 AB가 최대로 일치, 따라서 F(3)=2F(3)=2이다.

ABABA에선 ABA가 최대이므로 F(4)=3F(4)=3.

마지막으로 ABABAB에서 ABAB가 최대이므로 F(5)=4F(5)=4가 된다. (ABABAB가 아님!!)

구한 실패 함수 값들을 표로 나타내보면 다음과 같다.

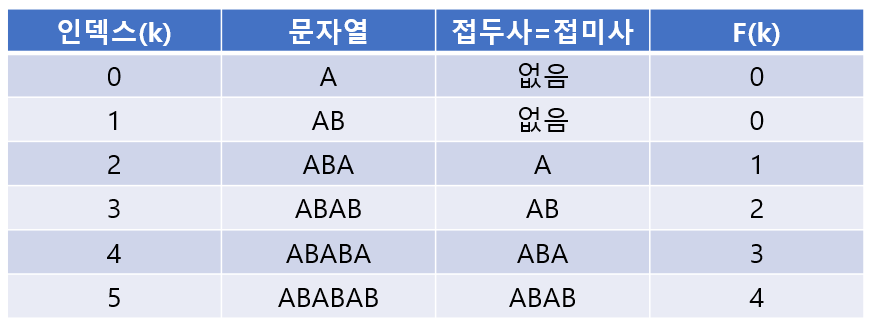
그럼 실패 함수값들을 KMP에서 어떻게 활용할 수 있을까?

★ KMP 알고리즘

드디어 KMP 알고리즘이 무엇인지 좀 더 명확히 알아볼텐데 SS는 방금 사용했던 ABABAB를 사용하고 HH는 좀 더 긴 문자열을 사용하기로 하자. 그리고 정확한 이해를 위해 변수 beginbegin을 HH의 시작 인덱스로, 일치하는 개수를 mm이라고 하면 아래와 같은 방식으로 동작한다.

  • H[begin+m]==S[m]H[begin+m]==S[m]: 일치할 경우, mm이 증가한다.
  • H[begin+m]!=S[m]H[begin+m]!=S[m]: 불일치할 경우, beginbegin이 스킵하는 만큼 증가하고 mm이 실패 함수값이 된다.

m=3m=3으로 3번째 인덱스에서 불일치가 발생한 경우이다. 이 경우엔 m−1m−1의 실패 함수 값을 확인하는데 mm개가 일치했다는 것은 인덱스 m−1m−1까지 일치했다는 말과 동일하기 때문이다. 위에서 구했던 것처럼 F(2)=1F(2)=1이기 때문에 다시 SS의 1번째 인덱스부터 비교하면 된다.

왜냐하면 F(2)=1F(2)=1이란 의미가 이전에 일치한 문자열 중에 접두사와 접미사가 일치하는 부분이 1개라는 뜻이기 때문에 0번째 인덱스가 일치한다는 것이 보장되기 때문이다. 따라서, m=1m=1로 초기화 되는데 이걸 일반화 하면 m=F(m−1)m=F(m−1)이 됨을 알 수 있다. 즉, 불일치가 발생할 경우엔 mm값이 실패 함수값으로 초기화된다.

또한 beginbegin 값을 옮겨주어야 하는데 beginbegin에 m−F(m−1)m−F(m−1)만큼 더해주면 된다. 이게 갑자기 왜 나왔냐 싶을지도 모르지만 생각해보면 일치하는 만큼(mm) 옮긴다음 반복되는 문자열의 길이 만큼(F(m−1)F(m−1)) 빼주는 개념이다. 위 예시에선 begin=0begin=0인 상태에서 m=3m=3을 더하면 begin=3begin=3이 되지만 F(m−1)=1F(m−1)=1을 빼주면 begin=2begin=2가 되기 때문에 알고리즘이 동작한다는 것을 확인할 수 있다.

m=1m=1로 옮겨진 후에 다시 비교해서 불일치가 발생하였다. F(1−1)=F(0)=0F(1−1)=F(0)=0이기 때문에 m=0m=0이되고 begin=2+1−0=3begin=2+1−0=3이 되서 다시 비교를 시작한다.

드디어 SS를 찾았는데 이 경우에는 단순히 완전히 건너뛰면 되는 것일까? 생각해보면, 완전히 일치하는 경우에도 접두사와 접미사가 일치하는 부분이 존재한다. 즉, 현재 m=6m=6인데 F(6−1)=F(5)=4F(6−1)=F(5)=4로 4개가 일치한다는 것을 알 수 있다. SS가 더 있을 가능성이 아직 남아있는 것이다. 따라서, m=4m=4로 초기화되고 begin=3+6−4=5begin=3+6−4=5가 되는데 5부터 남은 문자개수가 5개이기 때문에 종료하게 된다. 즉, beginbegin 값이 SS의 길이를 충족시킬 수 있을 때까지만 지속하는 것이다.

위의 모든 과정들을 이해했는가? 이해했으면 코드를 보도록 하자. (코드는 종만북을 참고!)

vector<int> kmp(const string& H, const string& S) 
{
    int h_len = H.length();
    int s_len = S.length();

    // 실패 함수값을 구해놓았다는 가정.
    vector<int> f = failure_function(S);
    vector<int> r(h_len-s_len+1,0);

    int begin = 0, m = 0;
    while(begin <= h_len-s_len) {
        // 일치개수(m)가 S의 길이보다 작고
        // H[begin+m]과의 문자가 일치하는 경우
        if(m<s_len && H[begin+m]==S[m]){
            m++;
            // S를 찾은 경우에 begin값을 저장한다.
            if(m == s_len) r.push_back(begin);
        }
        // 불일치하거나 S를 찾은 경우
        else {
            // 일치한적이 한번도 없고 불일치했다면 단순히 begin 옮기면 된다.
            if(m==0)
                begin++;
            // 그게 아니라면 begin과 m을 위에서 말한 것처럼 초기화!
            else {
                begin += (m - f[m-1]);
                m = f[m-1];
            }
        }
    }
    return r;
}

위 코드의 시간복잡도는 얼마나 될까? 최악의 경우 HH의 모든 문자를 봐야 하기 때문에 HH의 길이를 HLHL이라고 한다면 O(HL)O(HL)이 된다. 아직 실패 함수를 계산하는 경우를 고려하진 않았지만 그래도 원래의 브루토 포스 접근보다 훨씬 빠르다는 것을 알 수 있다.

★ 실패 함수를 구하자

일단, 실패 함수의 정의를 다시 한번 되새겨보자.

0번째 인덱스를 제외한 각 인덱스에서 해당 인덱스까지의 부분문자열 중 접두사와 접미사가 일치하는 최대 길이로 kk가 인덱스일 경우 F(k)F(k)로 나타낼 수 있다.

이 말을 단순하게 생각해보면 각 인덱스에서 접두사==접미사인 부분을 찾으라는 말이다. 그러나 문자열 단순 탐색이 비효율적이기 때문에 KMP에서 줄인 시간복잡도를 원상복귀 시키는 불상사가 발생할 수 있다.

그럼 어떻게 할 수 있을까? 자세히 들여다보면 KMP의 원리를 똑같이 쓸 수 있는데 그 이유를 확인해보자.

beginbegin과 mm을 똑같이 쓸텐데 헷갈릴 수 있으니 각 인덱스에서 그 값을 확인하자. 먼저 처음 값들이다.

  • begin=1begin=1
  • m=0m=0

H[begin+m]=H[1]H[begin+m]=H[1]이 S[m]=S[0]S[m]=S[0]과 불일치하고 m=0m=0이므로 beginbegin만 증가한다.

  • begin=2begin=2
  • m=0m=0

H[2]H[2]가 S[0]S[0]과 일치하기 때문에 mm이 증가하고 F[begin+m−1]=F[2]=1F[begin+m−1]=F[2]=1이 된다.

  • begin=2begin=2
  • m=1m=1

H[3]H[3]과 S[1]S[1]이 일치하기 때문에 mm이 증가하고 F[3]=2F[3]=2가 된다.

  • begin=2begin=2
  • m=2m=2

H[4]H[4]와 S[2]S[2]가 일치하기 때문에 mm이 증가하고 F[4]=3F[4]=3이 된다.

  • begin=2begin=2
  • m=3m=3

마지막으로 H[5]H[5]와 S[3]S[3]이 일치해서 mm이 증가하고 F[5]=4F[5]=4가 된 후에 종료된다.

  • begin=2begin=2
  • m=4m=4

여기서 주목할 점은 mm이 증가하게 될 때 beginbegin은 따로 증가하지 않는다는 점인데, 그 이유는 HH의 인덱스가 begin+mbegin+m으로 참조되기 때문이다. 불일치로 인해 실패 함수값을 쓰는 경우가 나오진 않았지만 원래의 KMP처럼 동작하기 때문에 똑같다고 할 수 있다.

이제 코드를 한번 확인해보자.

vector<int> failure_function(const string& S)
{
    int n = S.length();
    vector<int> f(n,0);
    int begin = 1, m = 0;

    // 끝까지 확인한다.
    while(begin+m < n) {
        // 일치하면 m을 증가시키고 실패함수를 초기화한다.
        if(S[begin+m]==S[m]) {
            m++;
            f[begin+m-1] = m;
        }
        else {
            if(m==0)
                begin++;
            else {
                begin += (m - f[m-1]);
                m = f[m-1];
            }
        }
    }
    return f;
}

사소한 부분을 제외하고는 거의 동일하게 동작한다는 것을 알 수 있다. 시간복잡도는 당연히 KMP를 활용하기 때문에 SS의 길이를 SLSL이라고 했을 때 O(SL)O(SL)만큼 나오게 된다. 결론적으로 KMP알고리즘의 최종 시간복잡도는 O(HL+SL)O(HL+SL)로 보통 HL≥SLHL≥SL인 점을 감안하면 O(HL)O(HL)이라고도 할 수 있다.

 

Reflection

  • 자바에서 이미 로딩이 완료된 클래스에서 또는 다른 클래스를 동적으로 로딩하여 구체적인 타입을 알지 못하더라도 생성자, 멤버 필드, 그리고 멤버 메소드를 사용할 수 있는 기법이다.
  • 객체를 통해서 클래스의 패키지 정보, 접근 지정자, 부모 클래스, 어노테이션 등을 얻을 수 있다.
  • 즉, 핵심은 컴파일 타임이 아니라 런타임에 동적으로 특정 클래스의 정보를 객체화하여 분석 및 추출해낼 수 있는 프로그래밍 기법이다.

[사용하는 이유는?]

  • 실행 시간(Runtime)에 다른 클래스를 동적으로 로딩하여 접근할 필요가 있을 때.
  • 클래스와 멤버 필드 그리고 메소드 등에 관한 정보를 얻어야할 때.
  • 리플렉션 없이도 완성도 높은 코드를 구현할 수 있지만, 사용한다면 조금 더 유연한 코드를 만들 수 있다.

[주의할 점]

  • 외부에 공개되지 않는 private 멤버도 Field.setAccessibile() 메소드를 통해 true로 지정하면 접근과 조작이 가능하기 때문에 주의해서 사용해야 한다.
  • Reflection에는 동적으로 해석되는 유형이 포함되므로 특정 JVM 최적화를 수행할 수 없다. 따라서 Reflection 작업이 비 Reflection 작업보다 성능이 떨어지며, 성능에 민감한 애플리케이션에서 자주 호출되는 코드엔 사용하지 않아야 한다.

 

인덱스

INDEX의 의미

  • RDBMS에서 검색 속도를 높이기 위해 사용하는 하나의 기술이다.
  • INDEX는 색인이다.
  • 해당 Table의 컬럼을 색인화(따로 파일로 저장)하여 검색시 해당 Table의 레코드를 full scan하는게 아니라 색인화 되어있는 INDEX 파일을 검색하여 검색 속도를 빠르게 한다.
  • INDEX 구조는 Tree 구조로 색인화한다.
  • RDBMS에서 사용하는 INDEX는 Balance Search Tree를 사용한다.

INDEX의 원리

INDEX를 해당 컬럼에 주게 되면 초기 Table 생성시, FRM, MYD, MYI 3개의 파일이 만들어진다.

  • FRM : 테이블 구조가 저장되어 있는 파일
  • MYD : 실제 데이터가 있는 파일
  • MYI : INDEX 정보가 들어있는 파일

INDEX를 사용하지 않는 경우, MYI 파일은 비어져 있다.

그러나 INDEX를 해당 컬럼에 만들게 되면 해당 컬럼을 따로 인덱싱하여 MYI 파일에 입력한다.

이후에 사용자가 SELECT 쿼리로 INDEX를 사용하는 쿼리를 사용시 해당 Table을 검색하는 것이 아니라 MYI 파일의 내용을 검색한다.

만약, INDEX를 사용하지 않은 SELECT 쿼리라면 해당 Table Full scan하여 모두 검색한다.

이는 책의 뒷부분에 <찾아보기>와 같은 의미로 정리해둔 단어 중에서 원하는 단어를 찾아서 페이지수를 보고 쉽게 찾을 수 있는 개념과 같다. 만약, 이 <찾아보기>가 없다면 처음부터 끝까지 모든 페이지를 보고 찾아와야할 것이다.

INDEX 장점

  • 키 값을 기초로 하여 테이블에서 검색과 정렬 속도를 향상시킨다.
  • 인덱스를 사용하면 테이블 행의 고유성을 강화시킬 수 있다.
  • 테이블의 기본키는 자동으로 인덱스된다.
  • 필드 중에는 데이터 형식 때문에 인덱스 될 수 없는 필드도 있다.
  • 여러 필드로 이루어진(다중 필드)인덱스를 사용하면 첫 필드 값이 같은 레코드도 구분할 수 있다.

참고로 액세스에서 다중 필드 인덱스는 최대 10개의 필드를 포함할 수 있다.

INDEX 단점

  • 인덱스를 만들면 .mdb 파일 크기가 늘어난다.
  • 사용자가 한 페이지를 동시에 수정할 수 있는 병행성이 줄어든다.
  • 인덱스된 필드에서 데이터를 업데이트하거나 레코드를 추가 또는 삭제할 때 성능이 떨어진다.
  • 인덱스가 데이터베이스 공간을 차지재 추가적인 공간이 필요해진다.(DB의 10% 내외의 공간이 추가로 필요하다.)
  • 인덱스를 생성하는데 시간이 많이 소요될 수 있다.
  • 데이터 변경 작업이 자주 일어날 경우에 인덱스를 재작성해야 할 필요가 있기에 성능에 영향을 끼칠 수 있다.

따라서 어느 필드를 인덱스해야 하는지 미리 시험해보고 결정하는 것이 좋다. 인덱스를 추가하면 쿼리 속도가 1초 정도 빨라지지만, 데이터 행을 추가하는 속도는 2초 정도 느려지게 되어 여러 사용자가 사용하는 경우, 레코드 잠금 문제가 발생할 수 있다.

또, 다른 필드에 대한 인덱스를 만들게 되면 성능이 별로 향상되지 않을 수도 있다. 예를 들어, 테이블에 회사 이름 필드와 성 필드가 이미 인덱스된 경우에 우편 번호를 필드로 추가해 인덱스에 포함해도 성능이 거의 향상되지 않는다. 만드는 쿼리의 종류와 관계 없이 가장 고유한 값을 갖는 필드만 인덱스해야 한다.

INDEX의 목적

RDBMS에는 INDEX가 있다. 인덱스의 목적은 RDBMS의 검색 속도를 높이는데 있다.

SELECT 쿼리의 WHERE절이나 JOIN 예약어를 사용했을 때만 인덱스를 사용하며, SELECT 쿼리의 검색 속도를 빠르게 하는데 목적을 두고 있다.

  • DELETE, INSERT, UPDATE 쿼리에는 해당 사항이 없으며 INDEX 사용시 오히려 좀 느려진다.

상황 분석

[사용하면 좋은 경우]

  1. Where절에서 자주 사용되는 Column

  2. 외래키가 사용되는 Column

  3. Join에 자주 사용되는 Column

[Index 사용을 피해야 하는 경우]

  • Data 중복도가 높은 Column
  • DML이 자주 일어나는 Column

DML에 취약

  1. INSERT

    • indext split : 인덱스의 Block들이 하나에서 두개로 나누어지는 현상.
    • 인덱스는 데이터가 순서대로 정렬되어야 한다. 기존 블록에 여유 공간이 없는 상황에서 그 블록에 새로운 데이터가 입력되어야 할 경우, 오라클이 기존 블록의 내용 중 일부를 새 블록에다가 기록한 후, 기존 블록에 빈 공간을 만들어서 새로운 데이터를 추가하게 된다.
    • 성능면에서 매우 불리하다.
      • Index split은 새로운 블록을 할당받고 Key를 옮기는 복잡한 작업을 수행한다. 모든 수행 과정이 Redo에 기록되고 많은 양의 Redo를 유발한다.
      • Index split이 이루어지는 동안 해당 블록에 대해 키 값이 변경되면 안되므로 DML이 블로킹된다.

  2. DELETE

    • 테이블에서 데이터가 Delete될 경우, 지워지고 다른 데이터가 그 공간을 사용할 수 있다.
    • index에서 데이터가 delete될 경우, 데이터가 지워지지 않고 사용 안됨 표시만 해둔다.
    • 즉, 테이블에 데이터가 1만건 있는 경우, 인덱스에는 2만건이 있을 수 있다는 뜻이다.
    • 인덱스를 사용해도 수행 속도를 기대하기 힘들다.

  3. UPDATE

    • 인덱스에는 Update 개념이 없다.
    • 테이블에 update가 발생할 경우, 인덱스에서는 delete가 먼저 발생한 후 새로운 작업의 insert 작업이 발생한다.
    • delete와 insert 두 개의 작업이 인덱스에서 동시에 일어나 다른 DML보다 더 큰 부하를 주게 된다.

참고

DB INDEX란?

저작자표시

'CS 공부 > CS Study 원본' 카테고리의 다른 글

CS - 20일차  (0) 2021.03.05
CS 19일차  (0) 2021.02.26
CS 17일차  (0) 2021.02.19
CS 16일차  (0) 2021.02.15
CS 15일차  (0) 2021.02.08
댓글 , 엮인글
코딩공부
블로그 이미지 맹털이 님의 블로그
MENU
CATEGORY
VISITOR 오늘 / 전체

티스토리툴바